Post

[ML] 2. 지도 학습 알고리즘(2-5) 다중 클래스 분류

Posted
By Jihyun,Ryu 9 min read

[ML with Python] 2. 지도 학습 알고리즘 (2) 다중 클래스 분류

  • 본 포스팅은 지도 학습 알고리즘인 분류용 선형 모델에 관한 기본적인 내용에 관하여 다룹니다.
  • 다중 클래스 분류용 선형 모델
  • 일대다 방법(one-vs.-rest)
  • SVC를 이용한 일대다 방법
  • 선형 모델의 매개변수 (정리)
  • 선형 모델의 장단점

필요 라이브러리 import

1
2
3
4
5
6
7

import mglearn
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC

다중 클래스 분류용 선형 모델

(로지스틱 회귀만을 제외하고) 많은 선형 분류 모델은 태생적으로 이진 분류만을 지원한다.
즉 다중 클래스(multiclass)를 지원하지 않는다는 의미이다. 그러므로, 이진 분류알고리즘을 다중 클래스 분류알고리즘으로 확장하기 위해서 주로 일대다 방법을 사용한다.


  • 일대다 방법(one-vs.-rest)
    • 이진 분류알고리즘을 다중 클래스 분류 알고리즘으로 확장하는 방법이다.
    • 각 클래스를 다른 모든 클래스와 구분하도록 이진 분류모델을 학습시킨다.
    • 결국 클래스의 수만큼 이진 분류모델이 만들어진다.
    • 예측할 때 이렇게 만들어진 모든 이진 분류기가 작동하여
      가장 점수가 높은 점수를 내는 분류기의 클래스를 에측값으로 선택한다.


클래스별 이진 분류기를 만들면 각 클래스가 계수 백터(w)와 절편(b)를 하나씩 가지게 된다.
결국 분류 신뢰도를 나타내는 다음 공식의 결과값이 가장 높은 클래스가 해당 데이터의 클래스 레이블로 할당된다.

w[0] × x[0] + w[1] × x[1] + … + w[p] × x[p] + b


다음 세 개의 클래스를 가진 데이터셋에 일대다 방식을 적용해보자
해당 데이터셋은 2차원이며 각 클래스의 데이터는 정규분포(가우시안 분포)를 따른다.

1
2
3
4
5

X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("property 0")
plt.ylabel("property 1")
plt.legend(["class 0", "class 1", "class 2"])

1

<matplotlib.legend.Legend at 0x188ccf92880>

linearmodel_multi_classification_model_5_1


먼저 LinearSVC 훈련결과를 확인해보자

1
2
3
4
5
6

linear_svm = LinearSVC().fit(X, y)
print(linear_svm.coef_)
print("계수 배열의 크기: ", linear_svm.coef_.shape)
print()
print(linear_svm.intercept_)
print("절편 배열의 크기: ", linear_svm.intercept_.shape)

1
2
3
4
5
6
7

[[-0.17492627  0.23141057]
 [ 0.4762129  -0.0693673 ]
 [-0.18914077 -0.20400584]]
계수 배열의 크기:  (3, 2)

[-1.07745602  0.13140337 -0.08604988]
절편 배열의 크기:  (3,)

  • coef_배열의 크기는 (3,2)이다.
    해당 배열의 행은 세 개의 클래스에 각각 대응하는 계수 벡터를 담고 있으며,
    열은 각 특성에 따른 계수 값을 가지고 있다.

  • intercept_는 각 클래스의 절편을 담고 있다.


세 개의 이진 분류기가 만드는 경계를 시각화하면 다음과 같다.

-(line * coef[0] + intercept) / coef[1]

위의 식은 기본적인 직선 공식(Ax+By+C = 0)에 기반되어있다.

coef[0]x + coef[1]y + intercept = 0
(coef[0]/coef[1])x + y + intercept/coef[1] = 0
y = -( (coef[0]/coef[1])x + intercept/coef[1] )

1
2
3
4
5
6
7
8
9
10
11

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
                                  mglearn.cm3.colors):
    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
    plt.ylim(-10, 15)
    plt.xlim(-10, 8)
plt.xlabel("property 0")
plt.ylabel("property 1")
plt.legend(['class 0', 'class 1', 'class 2', 'class 0 boundary', 'class 1 boundary',
            'class 2 boundary'], loc=(1.01, 0.3))

1

<matplotlib.legend.Legend at 0x188d3395910>

linearmodel_multi_classification_model_11_1

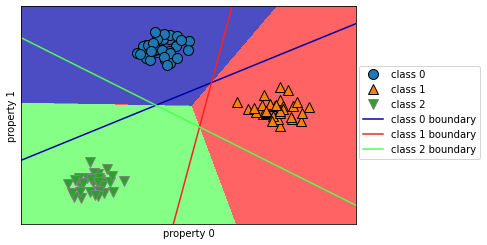
각각의 선이 이진 분류 모델을 뜻한다. 클래스의 수 만큼 이진 분류 모델이 만들어진 것을 확인할 수 있다. 이를 토대로 decision boundary가 그려진다.


그렇다면 위의 그림 중앙의 세 분류기가 모두 나머지로 분류한 삼각형 영역은 어떻게되는 걸까? 해당 데이터 포인트는 가장 가까운 직선의 클래스가 될 것이다.


다음 예는 2차원 평면의 모든 포인트에 대한 예측 결과를 보여준다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)


for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,    
                                   mglearn.cm3.colors):
    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)

    
    plt.legend(['class 0', 'class 1', 'class 2', 'class 0 boundary', 'class 1 boundary',
            'class 2 boundary'], loc=(1.01, 0.3))
plt.xlabel("property 0")
plt.ylabel("property 1")

1

Text(0, 0.5, 'property 1')

linearmodel_multi_classification_model_13_1

선형 모델의 매개변수

선형 모델의 주요 매개변수는 다음과 같았다.

  • 회귀 모델 : alpha
    • alpha ↑ => 모델이 단순해짐


  • LinearSVC와 LogisticRegression : C
    • C ↓ => 모델이 단순해짐


특별히 회귀 모델에서는 이 매개변수를 조정하는 것이 매우 중요하다.
보통 C와 alpha는 로그 스케일로 최적치를 정한다.


그리고 L1 규제를 사용할지 L2 규제를 사용할지도 정해야한다.

  • 중요한 특성이 많지 않음 => L1 규제
    • 특히, 해당 규제는 모델의 해석이 중요한 요소일 떄도 사용할 수 있다.
      몇 가지 특성만 사용하므로 해당 모델에 중요한 특성이 무엇이고 그 효과가 어느 정도인지 설명하기 쉬워진다.


  • 중요한 특성이 많음 => L2 규제

선형 모델의 장단점

장점

  • 학습 속도와 예측이 빠르다.


  • 매우 큰 데이터셋과 희소한 데이터셋에서도 잘 작동한다.
    • 수십만에서 수백만 개의 샘플로 이뤄진 대용량 데이터셋이라면 기본 설정보다 빨리 처리하도록 LogisticRegression과 Ridge에 solver='sag' 옵션을 준다.
    • 다른 대안으로 SDGClassifier와 SGDRegressor을 사용할 수 있다.


  • 회귀와 분류에서 본 공식을 사용해 예측이 어떻게 만들어지는지 비교적 쉽게 이해할 수 있다.


  • 샘플에 비해 특성이 많을 때 잘 작동한다.
    다른 모델로 학습하기 어려운 매우 큰 데이터셋에도 선형 모델을 많이 사용한다.

단점

  • 위에서 처럼 예측이 어떻게 만들어지는지 비교적 쉽게 이해할 수 있지만,
    계수의 값들이 왜 그런지는 명확하지 않을 때가 종종있다.
    특히 데이터셋의 특성들이 서로 깊게 연관되어 있을 때 그렇다.
    그리고 이런 경우 계수 분석이 매우 어려울 수 있다.


  • 특성이 적은 저차원 데이터셋에서는 다른 모델들의 일반화 성능이 더 좋다.

References

Data, Machine Learning
Data Machine Learning
This post is licensed under CC BY 4.0 by the author.