[자료구조] 3.재귀 알고리즘 (Recursive Algorithms)
재귀함수(Recursive Functions) 란?
- 하나의 함수 혹은 알고리즘을 반복적으로 호출하여 작업을 수행하는 성질을 의미한다.
재귀 알고리즘(Recursive Algorithm)이라고 불리는 것들이 있으나,
재귀(Recursive)자체는 알고리즘이 아니라성질에 해당한다.- 해당 성질을 이용해서 생각보다 많은 종류의 문제를 재귀적(Recursively)으로 해결할 수 있다.
- 더불어, 정상적으로 해결하기 위해서는
종결 조건(Trivial Case)에 대해서 반드시 명시해줄 필요하며, 해당 조건까지를 아울러재귀 알고리즘(Recursive Algorithm)이라한다. - 하지만, 재귀적으로 표현된 알고리즘은 직관적이지만, 실제 성능의 경우에는 재귀함수는 여러 번의 함수 호출이 발생되기 때문에 일반적인 반복(Iterative)보다 좋지 않은 경우가 더 많다.
(1) 예시: 등차수열
기본적인 등차 수열의 공식은 다음과 같으며, 최우측 항과 같이 재표기할 수 있다.
\[S=\displaystyle\sum_{k=1}^{n}k = n+\displaystyle\sum_{k=1}^{n-1}k \]
위의 최우측 항을 재귀함수로 작성 시 다음과 같이 작성할 수 있을 것 같다.
1
2
def sum(n):
return n + sum(n- 1)
하지만, 위의 함수를 동작시켰을 때, 기대와 달리 음의 정수까지 계산에 무한정 포함하다가 중단되는 것을 확인할 수 있다. 이러한 원인이 발생되는 이유는 위에서 언급한 종결 조건(Trivial Case)을 명시하지 않았기 때문이다.
하단은 종결 조건(Trivial Case)를 명시한 등차수열 재귀함수이다.
1
2
3
4
5
def sum(n):
if n <= 1:
return n
else:
return n + sum(n - 1)
추가적으로, 위에서 언급했듯이, 재귀(Recursive) 함수는 반복(Iterative) 함수보다 효율성이 떨어지는 경우도 많다. 다음은 등차수열을 재귀 및 반복함수로 표현하여 처리 시간을 비교한 코드이다. 두 함수의 복잡도는 모두 \(O(n)\)인 것을 확인할 수 있으며, 반복함수가 재귀함수보다 처리시간이 빨랐음을 확인할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import time
def recur_sum(n):
if n <= 1:
return n
else:
return n + recur_sum(n - 1)
def iter_sum(n):
s = 0
while n >= 0:
s += n
n -= 1
return s
if __name__ == "__main__":
n=100
recur_st = time.time()
recur_result = recur_sum(n)
recur_et = time.time()
print(f"(재귀)수행시간: {recur_et-recur_st}, 결과값: {recur_result}")
iter_st = time.time()
iter_result = iter_sum(n)
iter_et = time.time()
print(f"(반복)수행시간: {iter_et-iter_st}, 결과값: {iter_result}")
1
2
(재귀)수행시간: 6.4849853515625e-05, 결과값: 5050
(반복)수행시간: 2.5033950805664062e-05, 결과값: 5050
(2) 예시: 피보나치(Fibonacci)
다음은 피보나치 순열을 집계하는 재귀 함수 및 반복 함수이다. 위의 예시에서 보았던 등차수열과 마찬가지로 반복함수가 재귀함수보다 처리시간이 빠른 것을 확인할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import time
def recur_fibonacci(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return recur_fibonacci(n-2) + recur_fibonacci(n-1)
def iter_fibonacci(n):
f0 = 0
f1 = 1
iter = 0
while iter <= n-2:
f2 = f1+f0
f0 = f1
f1 = f2
iter += 1
return f2
if __name__ == "__main__":
n=10
recur_st = time.time()
recur_result = recur_fibonacci(n)
recur_et = time.time()
print(f"(재귀)수행시간: {recur_et-recur_st}, 결과값: {recur_result}")
iter_st = time.time()
iter_result = iter_fibonacci(n)
iter_et = time.time()
print(f"(반복)수행시간: {iter_et-iter_st}, 결과값: {iter_result}")
1
2
(재귀)수행시간: 3.62396240234375e-05, 결과값: 55
(반복)수행시간: 3.337860107421875e-06, 결과값: 55
(3) 예시: 이진 탐색(Binary Search)
다음은 이진 탐색(Binary Serach)에서 재귀함수를 적용한 경우에 대한 설명이다.
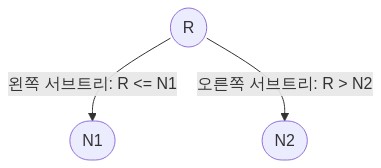
- 각 노드내에 정수형 숫자를 지니고 있으며 다음의 규칙을 요구하는 자료구조가 있다고 정의하자.
Root노드(R)를 기준으로
왼쪽 서브트리에 위치한 노드(N1)에는 R노드 내에 위치한 수 보다 작거나 같은 값이 위치하며,
우측 서브트리에 위치한 노드(N2)에는 R노드 내에 위치한 수 보다 큰 값이 위치한다.
위의 트리 구조를 모든 노드에 대해서 재귀적으로 적용하면, 이진 트리 구조를 만들어볼 수 있다.
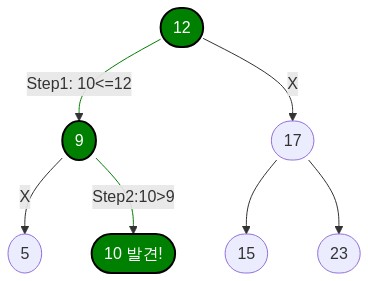
다음은 트리 구조를 통해 리스트 [5, 9, 10, 12, 15, 17, 23]에서 재귀적으로 원소 10을 찾는 예시이다.
다음은 이진 트리 구조를 재귀 함수로 나타낸 대략적인 코드이다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
def recur_bi_search(L, x, l, u): # x not in u의 경우에는 리스트의 길이에 비례하는 시간을 소요하기에 효율적이지 않다. if l > u: return -1 mid = (l+u)//2 if x == L[mid]: return mid elif x < L[mid]: return recur_bi_search(L, x, l, mid-1) else: return recur_bi_search(L, x, mid+1, l) if __name__ == '__main__': L = [2, 3, 5, 6, 9, 11, 15] x = 6 # 찾고자 하는 원소 l = 0 # 최소 범위 인덱스 u = 6 # 최대 범위 인덱스 print(recur_bi_search(L,x,l,u))