[ML] 2. 지도 학습 알고리즘(4-1) 결정 트리

Posted Nov 15, 2020

By Jihyun,Ryu 22 min read

[ML with Python] 2. 지도 학습 알고리즘 (4) 결정 트리

본 포스팅은 지도 학습 알고리즘인 결정 트리에 관한 기본적인 내용에 관하여 다룹니다.
결정 트리 (Decision Tree)
결정 트리의 복잡도 제어
- 사전 가지치기
- 사후 가지치기
결정 트리 분석과 특성 중요도
회귀 결정 트리(DecisionTreeRegression)
결정 트리의 장단점

필요 라이브러리 import

  
import mglearn
import graphviz
import pandas as pd
import numpy as np
import os
from matplotlib import pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

결정 트리(Decision Tree)

분류와 회귀 문제에 널리 사용하는 모델
기본적으로 결정에 다다르기 위해 예/아니오 질문을 이어 나가며 학습한다.(스무고개와 유사)

  
mglearn.plots.plot_animal_tree()

위 그림에서

트리의 노드 : 질문이나 정답을 담은 네모 상자, 마지막 노드의 경우 리프(leaf)라 한다.
트리의 엣지 : 질문의 답과 다음 질문을 연결

쉽게 말하자면 위의 질문들을 이용해 네 개의 클래스를 구분하는 모델을 만든 것이다.
이런 모델을 직접 만드는 대신 지도 학습 방식으로 데이터로부터 학습할 수 있다.

결정 트리 만들기

결정 트리를 학습한다는 것은 정답에 가장 빨리 도달하는 예/아니오 질문 목록을 학습한다는 의미이다.
머신러닝에서는 이런 질문들을 테스트라고 한다.

보통 데이터는 앞서의 동물 구분 예제와 같이 예/아니오 형태의 특성으로 구성되지 않고,
다음의 데이터와 같이 연속된 특성으로 구성된다.

연속적인 데이터에 적용할 테스트는 특성 i는 값 a보다 큰가?와 같은 형태를 보인다.

트리를 만들 때의 알고리즘은 가능한 모든 테스트에서
타겟 값에 대하여 가장 많은 정보를 가진 것을 고른다.
즉, 모든 테스트(질문)에서 데이터를 가장 잘 나누는 테스트(질문)을 찾는 것이다.

아래의 그림은 첫 번째로 선택된 테스트를 보여준다.
데이터셋을 x[1] = 0.06에서 수평으로 나누는 것이 가장 많은 정보를 포함한다.
즉 이 직선이 class 0와 class 1의 포인트를 가장 잘 나누는 것이다.

루트 노트(root node)라 불리는 맨 위의 노드는
class 0에 속한 포인트 50개와 class 1에 속한 포인트 50개를 모두 포함한 전체 데이터셋을 나타낸다.

첫 번째 분류가 두 class를 완벽하게 분류하지 못해서
아래 영역에는 아직 class 0에 속한 포인트가 들어 있고, 위 영역에는 class 1에 속한 포인트가 포함되어 있다.

이 두 영역에서 가장 좋은 테스트를 찾는 과정을 반복해서 모델을 더 정확하게 만들 수 있다.

반복된 프로세스는 각 노드(네모상자)가 테스트(질문) 하나씩을 가진 결정 트리를 만든다.
이는 계층적으로 영역을 분할해가는 알고리즘이라고 할 수 있다.
각 테스트는 하나의 특성에 대해서만 이루어지므로 나누어진 영역은 항상 축에 평행하다.

데이터를 분할하는 과정은 분할된 하나의 영역이 한 개의 타깃값을 가질 때까지 반복된다.
이때, 타깃 하나로만 이뤄진 리프노드를 순수 노드(pure node)라고 한다.

새로운 데이터 포인트에 대한 예측은
주어진 데이터 포인트가 특성을 분할한 영역들 중 어디에 놓이는지를 확인하면 된다.

같은 방법으로 회귀 문제에도 트리를 사용 가능하다.
예측을 하려면 각 노드의 테스트 결과에 따라 트리를 탐색해나가고
새로운 데이터 포인트에 해당되는 리프 노드를 찾는다.

찾은 리프 노드의 훈련 데이터 `평균 값`이 이 데이터 포인트의 출력이 된다.

결정 트리의 복잡도 제어하기

일반적으로 모든 리프 노드가 순수 노드가 될 때까지 진행된다면

모델이 매우 복잡해진다.
훈련 데이터에 과대적합된다.
즉 순수 노드로만 이루어진 트리는 훈련 세트에 100%정확하게 맞는다는 의미이다.

아래의 그래프에서 결정트리과정에서 과대적합의 예시이다. class 0으로 결정된 영역이 class 1에 속한 포인트들로 둘러쌓인 것을 볼 수 있다. 그 반대 모습도 보인다. 이는 바람직한 결정 경계가 아니다.

과대적합을 막는 전략은 크게 두 가지이다.

사전 가지치기(pre_pruning)
- 트리 생성을 일찍 중단
- 트리의 최대 깊이를 제한
- 분할하기 위한 포인트의 최소 개수를 지정
사후 가지치기(post-pruning)
- 트리를 만든 후 포인트가 적은 노드를 삭제하거나 병합시키는 전략

scikit-learn에서 결정 트리는 DecisionTreeRegressor와 DecisionTreeClassifier에 구현되어있다.
하지만, scikit-learn에서는 사전 가지치기만을 지원한다.

유방암 데이터셋을 이용해서 사전 가지치기의 효과를 확인해보자
기본값 설정으로 완전한 트리(모든 리프 노드가 순수 노드가 될 때까지 생성한 트리) 모델을 만들고,
random_state 옵션을 고정해 만들어진 트리를 같은 조건으로 비교할 것이다.

  
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=42)

tree = DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)

print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))

훈련 세트 정확도: 1.000
테스트 세트 정확도: 0.937

모든 리프 노드가 순수 노드이므로 훈련 세트의 정확도는 100%이다.
즉 트리는 훈련 세트의 모든 레이블을 완벽하게 기억할 만큼 완벽하게 만들어졌다.

결정 트리의 깊이를 제한하지 않으면 트리는 무한정 깊어지고 복잡해진다.
그래서 가지치기하지 않은 트리는 과대적합되기 쉽고 새로운 데이터에 잘 일반화되지 않는다.

이제 사전 가지치기를 트리에 적용해서 훈련 세트에 완전히 학습되기 전에 트리의 성장을 막아보자
max_depth=4 옵션을 주면 연속된 질문을 최대 4개로 제한한다.(즉 4번의 단계가 시행된다는 의미)
트리의 깊이를 제한하면 훈련 세트의 정확도를 떨어뜨리지만,
과대적합이 줄어들며, 테스트 세트의 성능을 개선시킨다.

  
tree = DecisionTreeClassifier(max_depth=4, random_state=0)
tree.fit(X_train, y_train)

print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))

훈련 세트 정확도: 0.988
테스트 세트 정확도: 0.951

결정 트리 분석

트리 모듈의 export_graphviz 함수를 이용해 트리를 시각화할 수 있다.
이 함수는 그래프 저장용 텍스트 파일 포맷인 .dot파일을 만든다.
각 노드에서 다수인 클래스를 색으로 나타내기 위해 옵션을 주고
적절히 레이블되록 클래스 이름과 특성 이름을 매개변수로 전달한다.

  
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree2.dot", class_names=["악성", "양성"],
                feature_names=cancer.feature_names,
                impurity=False, filled=True)

  
with open("tree.dot", encoding='UTF-8') as f:
    dot_graph = f.read()
display(graphviz.Source(dot_graph))

그러나 여기서 보듯이 깊이가 4만 되어도 트리는 매우 장황해진다.
트리가 더 깊어지면(10 정도의 깊이는 보통입니다) 한눈에 보기가 힘들어진다.
트리를 조사할 때는 많은 수의 데이터가 흐르는 경로를 찾아보면 좋다.

대부분의 양성 샘플은 왼쪽에서 두 번째 노드에 할당되고
나머지 리프 노드 대부분은 매우 적은 양의 샘플만 가지고 있다.

트리의 특성 중요도

전체 트리를 살펴보는 것은 어려울 수 있으므로,
대신 트리가 어떻게 작동하는지 요약하는 속성들을 사용할 수 있다.

가장 널리 사용되는 속성은 트리를 만드는 결정에
각 특성이 얼마나 중요한지를 평가하는 특성 중요도(feature importance)가 있다
이 값은 0과 1사이의 숫자이다.

0 : 전혀 사용되지 않았다는 의미
1 : 완벽하게 타깃 클래스를 예측했다는 의미
특성 중요도의 전체 합은 1이다.

  
print("특성 중요도:\n{}".format(tree.feature_importances_))

특성 중요도:
[0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.01019737 0.04839825
 0.         0.         0.0024156  0.         0.         0.
 0.         0.         0.72682851 0.0458159  0.         0.
 0.0141577  0.         0.018188   0.1221132  0.01188548 0.        ]

선형 모델의 계수를 시각화하는 것과 비슷한 방법으로 특성 중요도도 시각화할 수 있다.

  
def plot_feature_importances_cancer(model):
    n_features = cancer.data.shape[1]
    plt.barh(range(n_features), model.feature_importances_, align='center')
    plt.yticks(np.arange(n_features), cancer.feature_names)
    plt.xlabel("feature_importances")
    plt.ylabel("property")
    plt.ylim(-1, n_features)

plot_feature_importances_cancer(tree)

첫 번째 노드에서 사용한 특성(“worst radius”)이 가장 중요한 특성으로 나타낸다.
이 그래프는 첫 번째 노드에서 두 클래스를 꽤 잘 나누고 있다는 것을 의미해주고 있다.

그러나 어떤 특성의 feature_importance_ 값이 낮다고 해서
이 특성이 유용하지 않다는 뜻이 아니다.
단지 트리가 그 특성을 선택하지 않았을 뿐이며 다른 특성이 동일한 정보를 지니고 있어서일 수 있습니다.

또한, 선형 모델의 계수와 달리,
특성 중요도는 항상 양수이며 특성이 어떤 클래스를 지지하는지 알 수 없다.
즉 위에서는 worst radius가 중요하다고 하지만,
높은 반지름이 양성을 의미하는지 악성을 의미하는지 알 수 없다.
이는 특성과 클래스사이에 간단한 관계가 없을 수 있음을 의미한다.

  
tree = mglearn.plots.plot_tree_not_monotone()
display(tree)

Feature importances: [0. 1.]

아래의 그림은 y축 특성이 클래스 레이블과 복합적인 관계를 가지고 있는
결정 트리가 만든 2차원 데이터셋에서의 결정 경계이다.
그리고 위의 그림은 아래의 그림에 나타난 데이터로 학습한 결정 트리이다.

여기서도 worst radius처럼 x[1]과 출력 클래스와의 관계는 단순한 관계가 나타나 있지 않음을 보인다.
즉 “X[1] 값이 높으면 클래스 0이고 값이 낮으면 1”이라고(또는 그 반대로) 말할 수 없다는 것이다.

회귀 결정 트리(DecisionTreeRegression)

DecisionTreeRegression로 구현된 회귀 결정 트리에서도
결정 트리(DecisionTreeClassifiaction)와 비슷하게 적용된다.
하지만 회귀를 위한 트리를 사용하고 싶을 때는 짚고 가야할 한가지의 특별한 속성이 있다.

(Point!!)
DecisionTreeRegressor(그리고 모든 다른 트리 기반 회귀 모델)는
외삽(extrapolation), 즉 훈련 데이터의 범위 밖의 포인트에 대해 예측을 할 수 없습니다.
다음의 컴퓨터 메모리 가격 동향 데이터셋을 이용해 확인해보자.

  
ram_prices = pd.read_csv(os.path.join(mglearn.datasets.DATA_PATH, "ram_price.csv"))

plt.semilogy(ram_prices.date, ram_prices.price)
plt.xlabel("year")
plt.ylabel("price ($/Mbyte)")

Text(0, 0.5, 'price ($/Mbyte)')

y 축은 로그 스케일이다.
그래프를 로그 스케일로 그리면 약간의 굴곡을 제외하고는
선형적으로 나타나서 비교적 예측하기가 쉬워진다.

날짜 특성 하나만으로 2000년 전까지의 데이터로 부터 2000년 후의 가격을 예측해보자.
여기서는 두 모델 DecisionTreeRegressor와 LinearRegression을 비교하면서 볼 것이다.

  
# 2000년 이전을 훈련 데이터로, 2000년 이후를 테스트 데이터로 만듭니다.
data_train = ram_prices[ram_prices.date < 2000] 
data_test = ram_prices[ram_prices.date >= 2000]

# 가격 예측을 위해 날짜 특성만을 이용합니다.
X_train = np.array(data_train['date']).reshape(-1,1)
# 데이터와 타깃의 관계를 간단하게 만들기 위해 로그 스케일로 바꿉니다.
y_train = np.log(data_train.price)

tree = DecisionTreeRegressor().fit(X_train, y_train)
linear_reg = LinearRegression().fit(X_train, y_train)

# 예측은 전체 기간에 대해서 수행합니다.
X_all = np.array(ram_prices['date']).reshape(-1,1)

pred_tree = tree.predict(X_all)
pred_lr = linear_reg.predict(X_all)

# 예측한 값의 로그 스케일을 되돌립니다.
price_tree = np.exp(pred_tree)
price_lr = np.exp(pred_lr)

  
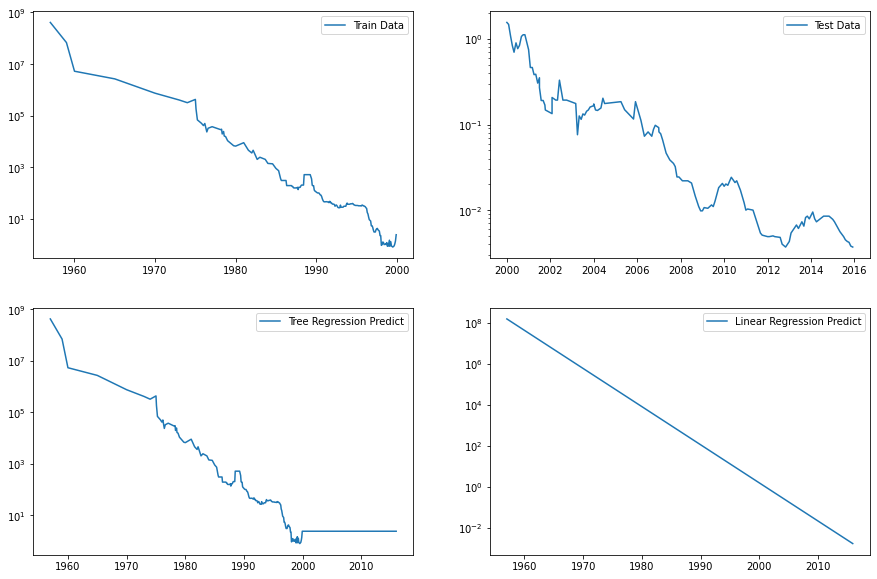
plt.figure(figsize=(15, 10))

plt.subplot(2,2,1)
plt.semilogy(data_train.date, data_train.price, label="Train Data")
plt.legend()

plt.subplot(2,2,2)
plt.semilogy(data_test.date, data_test.price, label="Test Data")
plt.legend()

plt.subplot(2,2,3)
plt.semilogy(ram_prices.date, price_tree, label="Tree Regression Predict")
plt.legend()

plt.subplot(2,2,4)
plt.semilogy(ram_prices.date, price_lr, label="Linear Regression Predict")
plt.legend()

<matplotlib.legend.Legend at 0x25ce0718d90>

  
plt.semilogy(data_train.date, data_train.price, label="Train Data")
plt.semilogy(data_test.date, data_test.price, label="Test Data")
plt.semilogy(ram_prices.date, price_tree, label="Tree Regression Predict")
plt.semilogy(ram_prices.date, price_lr, label="Linear Regression Predict")
plt.legend()

<matplotlib.legend.Legend at 0x25ce0419e50>

두 모델은 확연한 차이를 보인다.

선형 모델
- 직선으로 데이터가 근사하였다.
- 직선은 훈련 데이터와 테스트 데이터에 있는 미세한 굴곡을 매끈하게 근사하여
  2000년 이후의 테스트 데이터를 꽤 정확하게 예측했다.
트리 모델
- 복잡도에 제한을 두지 않았기 때문에 훈련 데이터를 완벽하게 예측한다.
- 모델이 가진 데이터 범위 밖(2000년 이후)으로 나가면 단순히 마지막 포인트를 이용해 예측해버린다.
- 트리 모델은 훈련 데이터 밖의 새로운 데이터를 예측할 능력이 없다.

장단점과 매개변수

결정 트리에서 모델 복잡도를 조절하는 매개변수로는 사전 가지치기 매개변수가 있다.

max_depth, max_leaf_nodes 또는 min_samples_leaf을 이용해 과대적합을 막음

결정 트리가 이전에 소개한 다른 알고리즘들보다 나은 점은 두 가지입니다

장점
- 만들어진 모델을 쉽게 시각화할 수 있고, 비전문가도 이해하기 쉽다.
- 데이터의 스케일에 구애받지 않는다.
- 각 특성이 개별적으로 처리되어있어 특성의 스케일이 달라도
  특성의 정규화나 표준화같은 전처리 과정이 필요없다.
- 특히 특성의 스케일이 서로 다르거나, 이진 특성과 같은 연속적인 특성이 혼합되어 있을 때도 잘 작동한다.

단점
- 사전 가지치기를 사용함에도 불구하고 과대적합되는 경향이 있어
  일반화 성능이 좋지 않다.

References

안드레아스 뮐러, 세라 가이도, 『파이썬 라이브러리를 활용한 머신러닝』, 박해선, 한빛미디어(2017)
https://tensorflow.blog/파이썬-머신러닝/2-3-5-결정-트리/

Data, Machine Learning

This post is licensed under CC BY 4.0 by the author.